John W Grun
Abstract
In this paper, a manually implemented LeNet-5 convolutional NN with an Adam optimizer written in Numpy will be presented. This paper will also cover a description of the data used to train and test the network,technical details of the implementation, the methodology of training the network and determining hyper parameters, and present the results of the effort.
Introduction
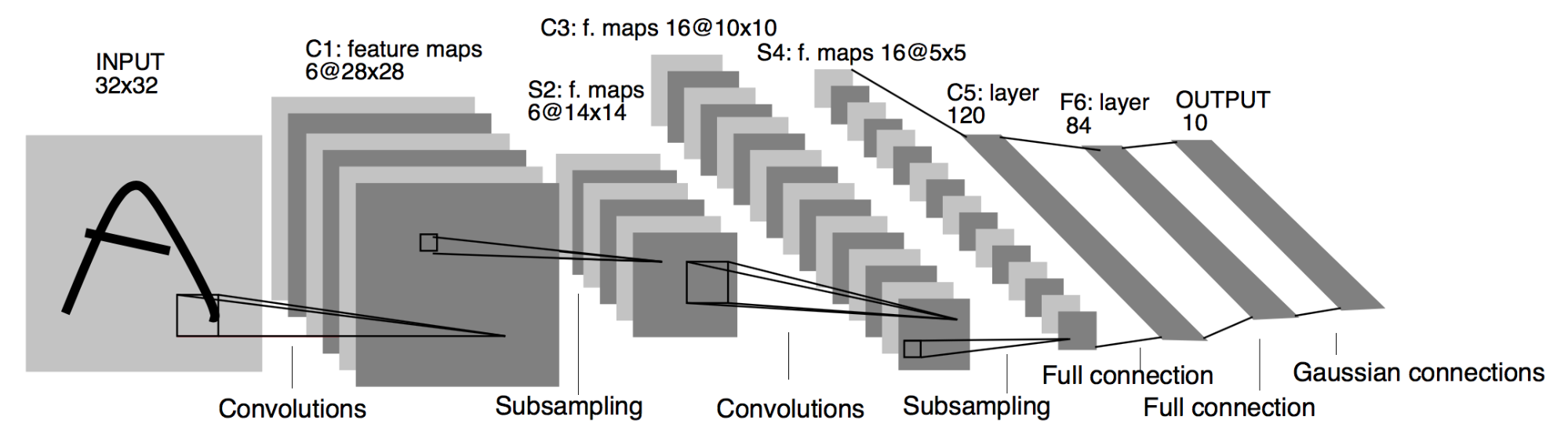
LeNet-5 was created by Yuan Lecun and described in the paper “Gradient-Based Learning Applied To Document Recognition” . LeNet-5 was one of the first convolutional neural networks used on a large scale to automatically classify hand-written digits on bank checks in the United States. Prior to LeNet, most character recognition was done by using feature engineering by hand, followed by a simple machine learning model like K nearest neighbors (KNN) or Support Vector Machines (SVM). LeNet made hand engineering features redundant, because the network learns the best internal representation from training images automatically.
This paper will cover some of the technical details of a manual Numpy implementation of LeNet-5 convolutional Neural Network including the details about the training set, structure of the lenet-5 CNN, weights and biases initialization, optimizer, gradient descent, the loss function, and speed enhancements. The paper will also cover the methodology used during training and selecting hyperparameters as well as the performance on the test dataset.
Related work
There are numerous examples of numpy implementations of LeNet 5 found across the internet but, none with more significance than any other. Lenet-5 is now a common architecture used to teach new students fundamental concepts of convolutional neural network
Data Description

The MNIST database of handwritten digits, contains a training set of 60,000 examples, and a test set of 10,000 examples. Each example is a 28 x 28 pixel grayscale image.
All training and test examples of the MNIST were converted from gray scale images to bilevel representation to simplify the function the CNN needed to learn. Only pixel positional information is required to correctly classify digits, while grayscale offers no useful additional information and only aids in increasing complexity. The labels of both the test and training examples were converted to one hot vectors to make them compatible with the softmax output and cross entropy loss function. Both indexes of the training and test sets were further randomized to ensure each batch was a random distribution of all 10 classes.
Model Description
Structure

The model is a implementation of LeNet 5 with the following structure:
- Input 28 x 28
- Convolutional layer (Pad = 2 , Stride = 1, Activation = ReLu, Filters = 6, Size = 5)
- Max Pool (Filter = 2, Stride = 2)
- Convolutional layer (Pad = 0 , Stride = 1, Activation = ReLu, Filters = 16 )
- Max Pool (Filter = 2, Stride = 2)
- Convolutional layer (Pad = 0 , Stride = 1, Activation = ReLu, Filters = 120)
- Fully Connected ( Size = 120, Activation = ReLu)
- Fully Connected (Size = 84, Activation = ReLu)
- Soft Max ( 10 Classes )
Weight and bias initialization
Since the original lenet-5 predates many of the more optimal weight initialization schemes such as Xavier or HE initialization, the weights were initialized with numpy random.randn while biases were zero filled with numpy zeros.
Optimizer
At first a constant learning rate optimizer was used for this network but, stable convergence required a very small learning rate. This small learning rate required a very long training time to achieve a reasonable accuracy on the test set. The constant learning rate optimizer was replaced with a numpy implementation of the ADAM optimizer. ADAM allowed for the use of higher learning rate that resulted in quicker and smoother convergence. The formulas that describe ADAM are shown below:
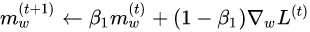
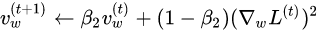
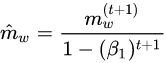
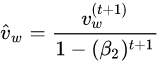
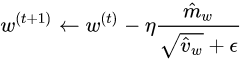
Gradient Descent
This implementation of LeNet-5 uses Mini-batch gradient descent. Mini-batch gradient descent is a trade-off between stochastic gradient descent (training on 1 sample at a time) and gradient descent (training on the entire training set). In mini-batch gradient descent, the cost function (and therefore gradient) is averaged over a small number of samples. Mini batch gradient descent was selected due to its increased convergence rate and the ability to escape local minimum.
Loss function
LeNet 5 produces a 10 class categorical output representing the numbers 0 to 9. The original LeNEt-5 used Maximum a posteriori (MAP) as the loss loss function. Cross-entropy was chosen as the loss function in this implementation instead of MAP since cross entropy appears to be the dominant loss function for similar classification problems and source code was available to check against. The formula for cross entropy loss is given below:
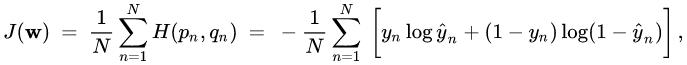
Speed Enhancements
To train the CNN in a reasonable amount of time several performance enhancements had to be made.
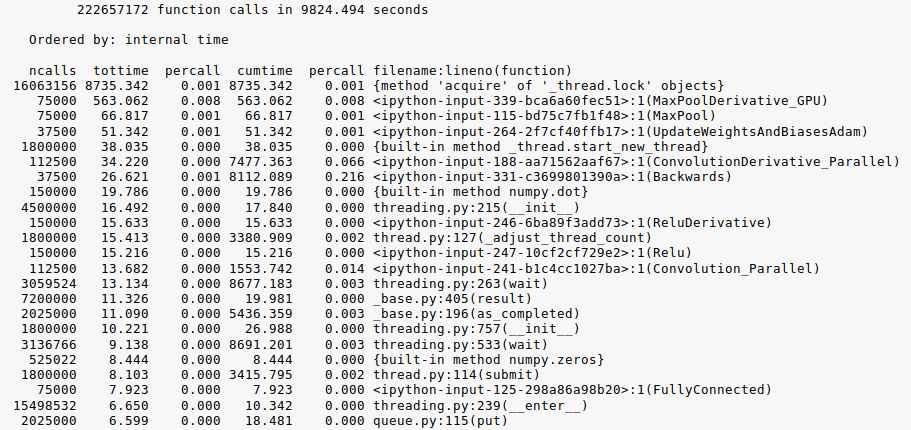
The python profiler was used to identify locations in the code that would have the largest effect on performance. The convolutional and max pooling layers consumed the majority of the running time. The running time of the convolutional and max pool layers was decreased by first converting the single threaded functions into multithreaded functions. Processing was divided up equally across the number of threads. Once threading was confirmed to be working properly, the Numba Just in Time compiler (JIT) was employed to convert python functions into native code. Numba JIT was then liberally applied throughout the code. These enhancements reduced the training time from over 1 day to a few hours, constituting a 6-8x speed up on average.
Method Description And Experimental Procedure
The LeNet 5 model implementation was trained on the MNIST dataset. After each training, the training loss versus epoch was plotted. The learning rate was decreased until the training loss vs epochs was a monotonically decreasing function. The number of epochs was selected to minimize the training loss while the training loss continued to decrease with every training epoch. Adjustments to the epochs sometimes also required adjustments to the learning rate to keep the training loss vs epoch a monotonically decreasing function.
In addition to the training loss, the prediction accuracy was computed. The accuracy was computed by the following method:
The input images were forward propagated through the network with the weights and biases learned during training. The class with the largest magnitude was selected as the prediction. The predicted class was compared to the label for a given input image. The percentage of correct predictions was computed across all input images forward propagated through the network.
The prediction accuracy was computed for both the training and testing sets . In a well trained network (one not underfitting or overfitting ) the test prediction accuracy should be close to the training prediction accuracy. If the training prediction accuracy is far greater than the test prediction accuracy it is a sign the network is overfitting on the training data and failing to generalize well.
The batch size was selected primary upon the cache limitations of the processor. A batch size of around 32 was determined to be small enough to fit in cache while also large enough to reduce overhead from thread context switching.
Results
Hyper parameters
The hyper parameters for this numpy implementation of LeNet 5 are as follows:
- Epochs = 20
- Learning rate = 0.0002
- Batch = 32
Training time
The total training time was brought down from 26 hours to train on the entire training set of 60000 examples to only 2.75 hours after applying speed enhancements.
Training loss
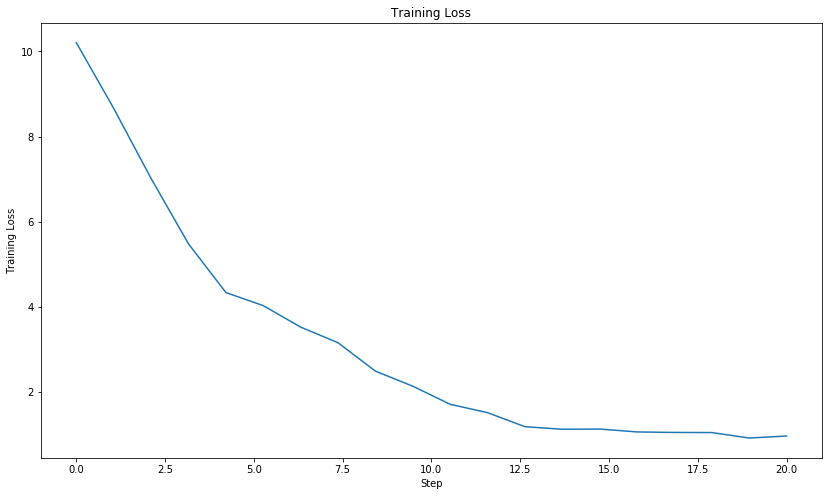
The training loss of LeNet-5 as plotted over 20 epochs. The training loss is monotonically decreasing indicating the network is effectively learning to differentiate between the ten classes in the MNIST dataset.
Accuracy
Accuracy on test set = 95.07%
Accuracy on Train set = 94.90%
The Lenet-5 implementation achieved a high accuracy on the test and train sets without a significant difference in prediction accuracy between the train and test sets which would be an indication of overfitting.
Conclusion
A Lenet 5 Convolutional Neural Network has been implemented only using Numpy that yields prediction accuracies over 95% on the test set. The network was trained on all 60000 examples found in the MNIST dataset and tested against the 10000 examples in the MNIST test set. The network used the standard LeNet Architecture with modifications where required. To decrease convergence time, a numpy ADAM optimizer was written. Several speed enhancements such as multi threading and just in time compilation were employed to decrease training time to a reasonable period.
References
[1] Lavorini, Vincenzo. “Speeding up Your Code (4): in-Time Compilation with Numba.” Medium, Medium, 6 Mar. 2018, medium.com/@vincenzo.lavorini/speeding-up-your-code-4-in-time-compilation-with-numba-177d6849820e.
[2] “Convolutional Neural Networks.” Coursera, www.coursera.org/learn/convolutional-neural-networks.
[3] LeCun, Yann. MNIST Demos on Yann LeCun’s Website, yann.lecun.com/exdb/lenet/.
[4] Lecun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324. doi:10.1109/5.726791
[5] “MNIST Database.” Wikipedia, Wikimedia Foundation, 11 Apr. 2019, en.wikipedia.org/wiki/MNIST_database.
[6] “Cross Entropy.” Wikipedia, Wikimedia Foundation, 8 May 2019, en.wikipedia.org/wiki/Cross_entropy.
[7] “Stochastic Gradient Descent.” Wikipedia, Wikimedia Foundation, 29 Mar. 2019, en.wikipedia.org/wiki/Stochastic_gradient_descent.